از تعریف یک کره می‌دانیم که فاصله نقاط واقع بر سطح آن از مرکزش برابر است. اما در مورد زمین هرچه از استوا دور شده و به قطبین نزدیک می‌شویم، فاصله نقاط از مرکز زمین کمتر می‌شود. بنابراین زمین یک کره نیست. شعاع استوایی زمین در حدود 6378 و شعاع قطبی آن در حدود 6356 کیلومتر است. همان‌طور که ملاحظه می‌شود، تغییرات شعاع نسبت به میانگین آن بسیار کوچک و می‌توان گفت که زمین به یک کره بسیار شبیه است. از آنجایی‌که تفاوت شکل زمین با یک کره واقعی، در جهت قبله اکثر نقاط زمین تأثیر ناچیزی دارد، در این نوشتار فرض می‌شود که زمین یک کره کامل است.
تصور کنید که بر روی یک صفحه بزرگ و در نقطه A قرار دارید. اگر در یک جهت دل‌خواه به حرکت درآیید و در طول مسیر به چپ یا راست منحرف نشوید، درواقع درحال طی بخشی از یک خط راست هستید. در این‌صورت اگر به نقطه B برسید، می‌توانیم بگوییم که AB یک پاره‌خط راست است. برای رفتن ازA به B می‌توانستید مسیرهای دیگری را هم برگزینید ولی هم راه شما طولانی‌تر می‌شد و هم در طول مسیر مجبور می‌شدید برای یک بار هم که شده به چپ یا راست منحرف شوید.
حال اگر به‌جای یک صفحه بر روی سطح یک کره قرار داشته باشیم و بخواهیم از نقطه A به نقطه B برویم و کوتاه‌ترین مسیر ممکن را طی کنیم، از بین بی‌شمار مسیر ممکن کدام را باید برگزینیم؟ جواب این است که در مورد کره، پاره‌خط راست جای خود را به کمانی از یک دایره عظیمه می‌دهد.
اگر کره‌ای با یک صفحه قطع داده‌شود، محل تلاقی، یک دایره خواهد بود که شعاع آن به فاصله صفحه از مرکز کره بستگی دارد. هرچه این فاصله بیشتر باشد، شعاع دایره حاصل کمتر خواهد بود. اگر صفحه از مرکز کره بگذرد دایره حاصل، دایره عظیمه است که بیشترین شعاع ممکن (همان شعاع کره) را داشته، کره را به دو قسمت برابر (دو نیم‌کره) تقسیم می‌کند.
در جای خود ثابت می‌شود که اگر نقاط A و B بر دو سر یک قطر کره واقع نشده باشند (خط واصل بین آن‌ها از مرکز کره نگذرد)، یک و فقط یک دایره عظیمه بر روی کره می‌توان ترسیم کرد که از این نقاط عبور کند. دایره مذکور توسط این نقاط به دو کمان نابرابر تبدیل می‌شود که طول کمان کوتاه‌تر همان کمینه فاصله ممکن بین نقاط A و B بر روی سطح کره می‌باشد. درصورتی که نقاط مذکور بر دو سر یک قطر کره واقع شده باشند (خط واصل بین آن‌ها از مرکز کره بگذرد)، می‌توان بی‌نهایت دایره عظیمه گذرنده از این نقاط را بر روی کره در نظر گرفت. بنابراین در این حالت کمینه فاصله ممکن، بی‌شمار جواب خواهد داشت.
اگر بر روی یک کمان از دایره عظیمه از نقطه A به نقطه B ره‌سپار شویم باز هم مانند طی کردن پاره‌خط راست بر روی صفحه، در هیچ نقطه‌ای از مسیر به چپ یا راست منحرف نخواهیم شد.
حال اگر نقطه A همان نقطه‌ای از سطح کره زمین باشد که می‌خواهیم جهت قبله را در آن معین کنیم و نقطه B هم محل خانه کعبه باشد، جهت مسیر دارای کمینه فاصله بین این دو نقطه همان جهت قبله است. البته با توجه به آنچه که پیش‌تر گفته شد، فرض می‌کنیم که نقطه A نقطه مقابل خانه کعبه در دیگرسوی کره زمین نیست، زیرا در این‌صورت، جهت قبله به هر سو که در نظر گرفته شود، صحیح خواهد بود.
با توجه به آنچه که گفته شد، برای محاسبه سمت قبله در یک نقطه مفروض، باید طول و عرض جغرافیایی آن نقطه و نیز مختصات جغرافیایی کعبه را بدانیم و سمت قبله را نسبت به شمال حقیقی در نقطه مورد نظر تعیین کنیم (بدین ترتیب، سمت شمال صفر، شرق 90، جنوب 180، غرب 270 و مجدداً شمال 360 یا همان صفر درجه خواهد بود).
فرض می‌کنیم که طول و عرض جغرافیایی نقطه مورد نظر (نقطه A)
به‌ترتیب برابر مبانی محاسبه جهت قبله و طول و عرض جغرافیایی خانه کعبه (نقطه A) 
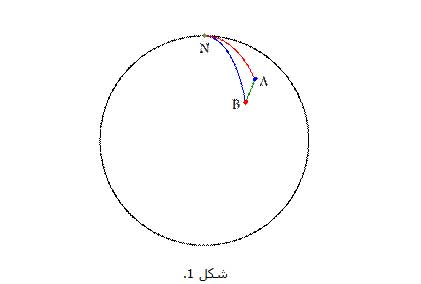
به‌ترتیب برابر مبانی محاسبه جهت قبله باشد. حال اگر قطب شمال جغرافیایی را N نامیده و مثلث کروی NAB را که هر سه ضلع آن کمان‌هایی از دوایر عظیمه گذرنده از این سه نقطه هستند، تشکیل دهیم، با محاسبه زاویه A (زاویه بین کمان‌های AN و AB) می‌توانیم سمت قبله را مشخص کنیم(شکل1). در صورتی که نقطه A تا 180 درجه غرب کعبه واقع شده باشد خود زاویه A و اگر تا 180 درجه شرق آن واقع شده باشد A-360، سمت قبله خواهد بود.
برای محاسبه زاویه A از روابط مثلثات کروی استفاده کرده، موارد زیر را در نظر می‌گیریم:
رابطه مورد استفاده هم از این قرار است:
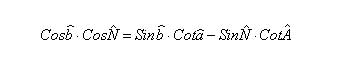که تنها مجهول آن زاویه A است. با جای‌گذاری خواهیم داشت:
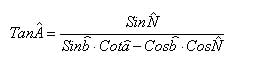اگر به‌عنوان مثال سمت قبله برای تهران مورد نظر باشد، معلومات ما بدین شرح است:
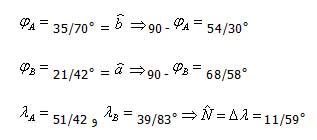که اگر این مقادیر را در رابطه بالا قرار دهیم خواهیم داشت:
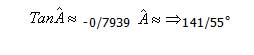و همان‌طور که قبلاً هم گفته شد، چون تهران در شرق خانه کعبه واقع شده است، داریم:
که اگر آن را با سمت جنوب (˚180) مقایسه کنیم درمی‌یابیم که جهت قبله در تهران از جنوب به اندازه ˚45/38 به‌سمت غرب متمایل شده‌است.
